Axe et centre instantanés de rotation (A.I.R.G et C.I.R.)
Axe instantané de rotation
Définition :
L'axe instantané de rotation d'un solide
par rapport à
(aussi appelé Axe Instantané de Rotation et de Glissement : A.I.R.G.) correspond à l'axe central du torseur cinématique de
par rapport à
.
D'une façon générale, on peut considérer qu'à tout instant, un mouvement quelconque de
est composé d'une rotation autour de cet axe et d'une translation rectiligne le long de cet axe.
Attention cependant, la position et l'orientation de cet axe évolue dans le temps.
Remarque :
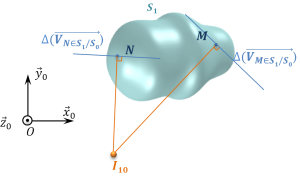
Pour déterminer la position de cet axe, on utilise la définition de l'axe central d'un torseur appliqué au torseur cinématique :
Soit le torseur
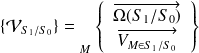
L'axe instantané de rotation d'un solide
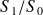est l'ensemble des points C tels que :
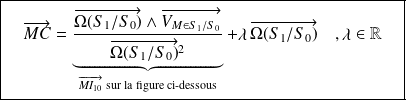
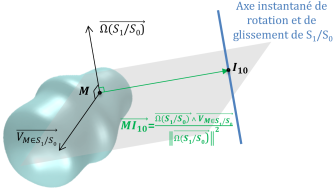
CIR pour un solide en mouvement plan
Définition : Centre instantané de rotation (C.I.R)
Soient deux solides
et
en mouvement plan sur plan de normale
.
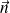A un instant
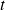, il existe un unique point noté
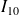, intersection de l'axe instantané de rotation et du plan de construction, tel que le solide
ait un mouvement de rotation autour de l'axe
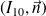par rapport à
.
Le point
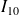est appelé Centre Instantané de Rotation (C.I.R.) de
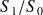. On peut montrer qu'à tout instant
,
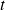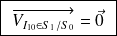
Attention :
Dans le cas général, le CIR se déplace quand le mécanisme change de position.
Complément : Démonstration
Dans le cas particulier d'un mouvement plan, la direction des vecteurs vitesse et taux de rotation permet d'affirmer que l'invariant scalaire est nul.
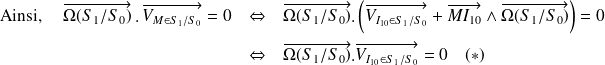
Par définition de l'axe central,
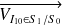et
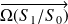sont colinéaires.
Ainsi, d'après
, si
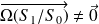alors
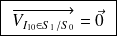
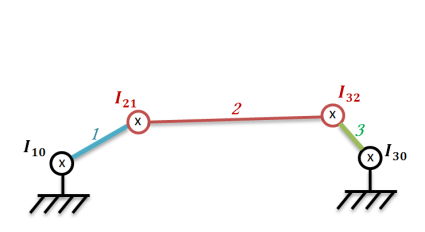
Applications graphiques du CIR
Intérêt du centre instantané de rotation (CIR)
Lorsque le CIR
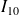d'un solide
en mouvement plan sur plan par rapport à un solide
est connu, tout se passe comme si à cet instant le solide
possédait un mouvement rotation de centre
.
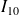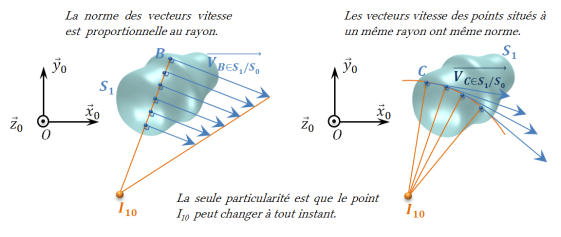
La méthode graphique présentée au paragraphe 2.2 dans le cadre du champ des vecteurs vitesse d'un solide en mouvement de rotation d'axe fixe peut alors être utilisée en considérant le point
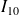comme centre de la rotation de
, mais à cet instant uniquement.
Connaissant la position de
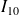et un vecteur vitesse en un point quelconque de
en mouvement par rapport à
, il est alors possible de construire le vecteur vitesse en tout point du
par rapport à
.
Détermination de la position du centre instantané de rotation (CIR)
Méthode : Recherche du CIR
|  |
Remarque :
Dans le cas d'un solide animé d'un mouvement de rotation autour d'un axe fixe, le CIR reste inchangé au cours du temps.
Dans le cas d'un solide animé d'un mouvement de translation, le CIR existe mais il est « rejeté à l'infini ». Ceci s'explique en assimilant une translation à une rotation de rayon infini.
A l'instant
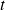correspondant à la position du mécanisme étudié, tout ce passe comme si les solides
et
étaient en rotation l'un par rapport à l'autre autour de leur CIR
.
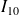Dans le cas du roulement sans glissement de
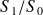en un point
,
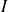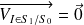. Ainsi le point de contact
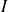correspond au CIR de
.
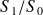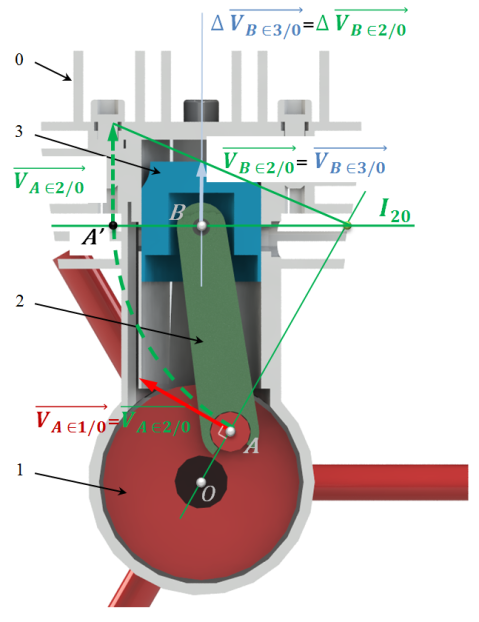
Exemple : Micromoteur de modélisme
On suppose que
,
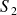et
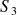ont des mouvements plans sur plans de normale
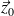par rapport au carter
. On donne
et le support
.
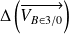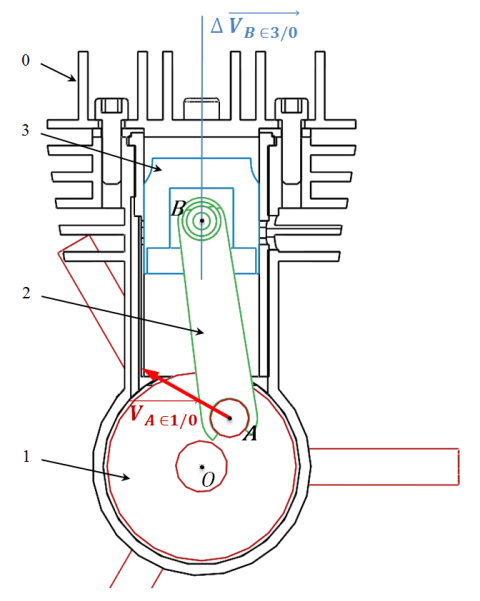
→ Déterminer graphiquement la position du CIR de
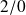noté
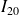et en déduire
.
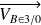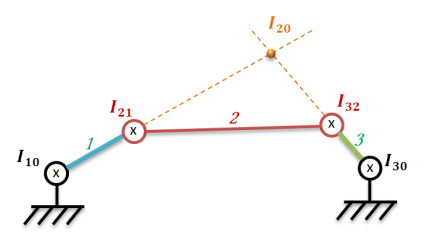
Théorème des trois plans glissants
Fondamental :
Soit
,
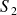et
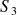trois solides en mouvement plan sur plan de normale
.
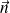On note
,
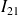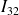et
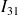les centres instantanés de rotation des mouvements relatifs de
,
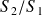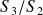et
.
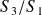Exemple :
→ Déterminer graphiquement la position du CIR du mouvement de
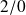noté
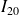à l'aide du théorème des trois plans glissants.
