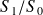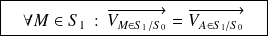Champ des vecteurs vitesse
Mouvement de translation
Rappel :
Le champ des vitesses d'un solide
en mouvement de translation par rapport à un solide
est uniforme.
Méthode : Application graphique
Connaissant :
on peut construire graphiquement le vecteur vitesse de tout point M de
|  |
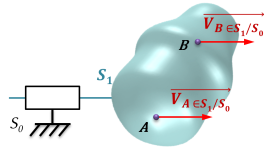Exemple : Micromoteur de modélisme
On suppose que le piston
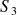est en mouvement plan sur plan de normale
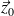par rapport au carter
. Le mouvement de
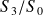peut alors être assimilé à une translation rectiligne de direction
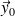. On donne
.
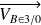→ Déterminer graphiquement
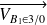et
.
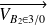Mouvement de rotation
Rappel :
Soit un solide
en mouvement de rotation d'axe
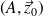par rapport à à
, à une vitesse angulaire
:
;
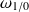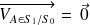les vecteurs vitesse des points liés à
/
sont tangents à la trajectoire et donc dans ce cas perpendiculaires aux « rayons » et à l'axe de rotation
;
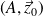la norme d'un vecteur vitesse est proportionnelle à la distance à l'axe (=rayon
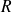) et à la vitesse angulaire :
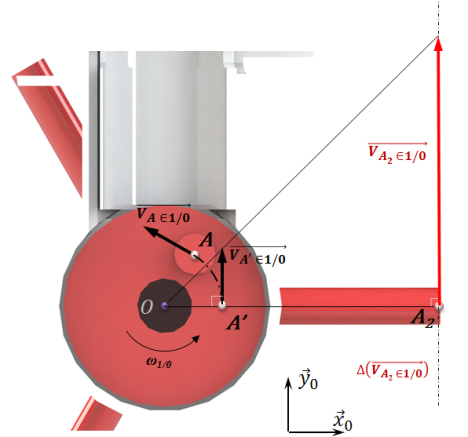
Méthode : Champ des vecteurs vitesse
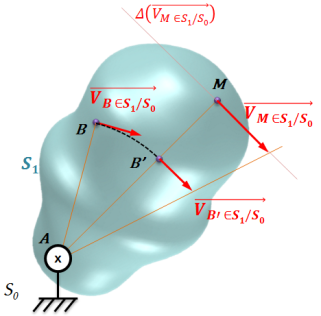
Connaissant :
le vecteur vitesse en un point
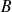de
dans en mouvement de rotation de centre
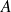par rapport à
:
,
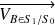on peut construire graphiquement le vecteur vitesse d'un point
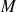quelconque de
/
:
On trace la droite
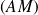.On construit sur la droite (AM) un point B' situé au même rayon que le point
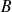.On trace
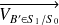, perpendiculaire à
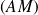et de même norme que
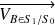car situé au même rayon.On trace le support (point d'application + direction) de
noté
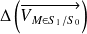.On trace le triangle des vitesses traduisant la répartition linéaire des vitesses pour un mouvement de rotation :
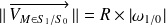
On en déduit
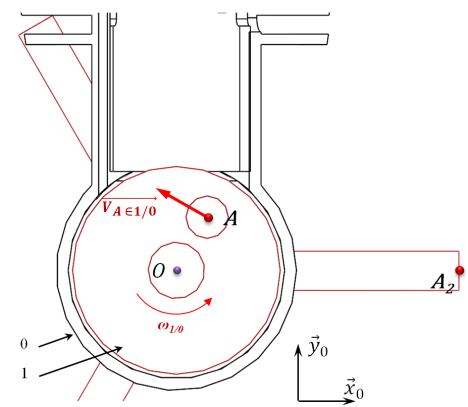
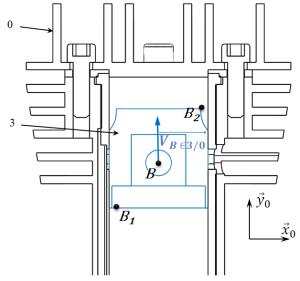
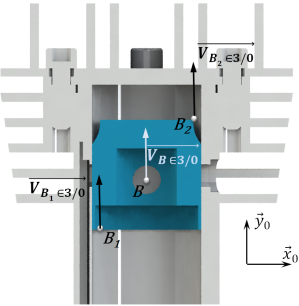
Exemple : Micromoteur de modélisme
Le mouvement du vilebrequin
par rapport au carter
est une rotation d'axe
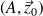. On donne
.
→ Déterminer graphiquement
.
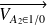