C03_P2 : Cinématique Graphique - Cas du mouvement plan

Afficher le planAfficher le plan

Définition du mouvement plan

DéfinitionMouvement plan sur plan

Le mouvement d'un solide par rapport à un solide est dit « plan sur plan », s'il existe un plan 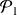lié au solide qui reste constamment confondu avec un plan lié solide .

Conséquences :

Soit un solide auquel on associe le repère 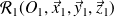en mouvement plan sur plan de normale 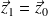par rapport à un solide auquel on associe le repère .

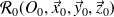  • La trajectoire d'un point 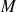quelconque lié à dans son mouvement par rapport à est contenue dans un plan perpendiculaire à

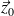
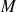  • Le torseur cinématique de par rapport à en un point quelconque est de la forme :

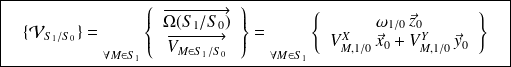
\boxed{\quad \{ \mathcal V_{S_1/S_0} \} ={\vphantom{\left\{\begin{array}{ccc}\overrightarrow{\Omega(S_1/S_1)}\\\overrightarrow{V(M\in S_2/S_1)}\\\end{array}\right\}}}_{\forall M \in S_1} \left \{ \begin{array}{c} \overrightarrow{\Omega(S_1/S_0)} \\ \overrightarrow{V_{M\in S_1/S_0}}\end{array} \right \} ={\vphantom{\left\{\begin{array}{ccc}\overrightarrow{\Omega(S_2/S_1)}\\\overrightarrow{V(M\in S_2/S_1)}\\\end{array}\right\}}}_{\forall M \in S_1} \left \{ \begin{array}{c} \omega_{1/0} \, \vec z_0 \\ V_{M,1/0}^X \, \vec x_0 +V_{M,1/0}^Y \, \vec y_0\end{array} \right \} \quad}

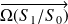  • reste à tout instant colinéaire à 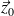(ou perpendiculaire au plan ).

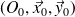  • Quelque soit le point 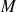lié à , reste perpendiculaire à 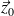(ou parallèle au plan ).

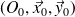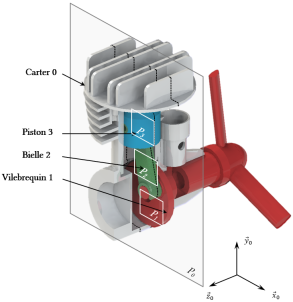
ExempleMicromoteur de modélisme

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimerRéalisé avec Scenari (nouvelle fenêtre)